圓周率π，我們都知道它是一個(gè)無(wú)理數(shù)。何為無(wú)理數(shù)？就是無(wú)限不循環(huán)小數(shù)，既然是無(wú)限不循環(huán)，當(dāng)然是不可能被完全算出來(lái)的，不可能用小數(shù)準(zhǔn)確地表示出來(lái)。

其實(shí)問題中“被完全算出來(lái)”的說法本身就是不嚴(yán)謹(jǐn)?shù)?，帶有?qiáng)烈的主觀色彩。何為“被完全算出來(lái)”？不一定非得用小數(shù)寫出來(lái)才是“完全被算出來(lái)”，其實(shí)圓周率π早已經(jīng)“被算出來(lái)”了，它就是π，就好比“1就是1”一樣，π和1在數(shù)學(xué)概念是上平等的，就是無(wú)理數(shù)和有理數(shù)之分而已，是確確實(shí)實(shí)存在的數(shù)，而且是非常固定的數(shù)。

由于π不能用小數(shù)完全算出來(lái)，總會(huì)讓一些人產(chǎn)生錯(cuò)覺，會(huì)認(rèn)為π是一個(gè)不固定的數(shù)。事實(shí)上π當(dāng)然是一個(gè)固定的數(shù)，還是那句話，π就是π，就如同“1就是1”一樣。

如果π不是固定的數(shù)，那么1/3也不是固定的數(shù)，因?yàn)?/3也不能完全用小數(shù)算出來(lái)。

任何無(wú)理數(shù)都可以在數(shù)軸上用線段的形式表示出來(lái)，比如說你可以非常輕松地畫出π厘米的線段，或者√2厘米長(zhǎng)的線段。數(shù)軸上的每一個(gè)點(diǎn)都對(duì)應(yīng)著一個(gè)實(shí)數(shù)，而實(shí)數(shù)包括有理數(shù)和無(wú)理數(shù)。雖然有理數(shù)和無(wú)理數(shù)都有無(wú)窮多個(gè)，但無(wú)理數(shù)的無(wú)窮比有理數(shù)的無(wú)窮要大得多！

下面重點(diǎn)說說無(wú)理數(shù)π。

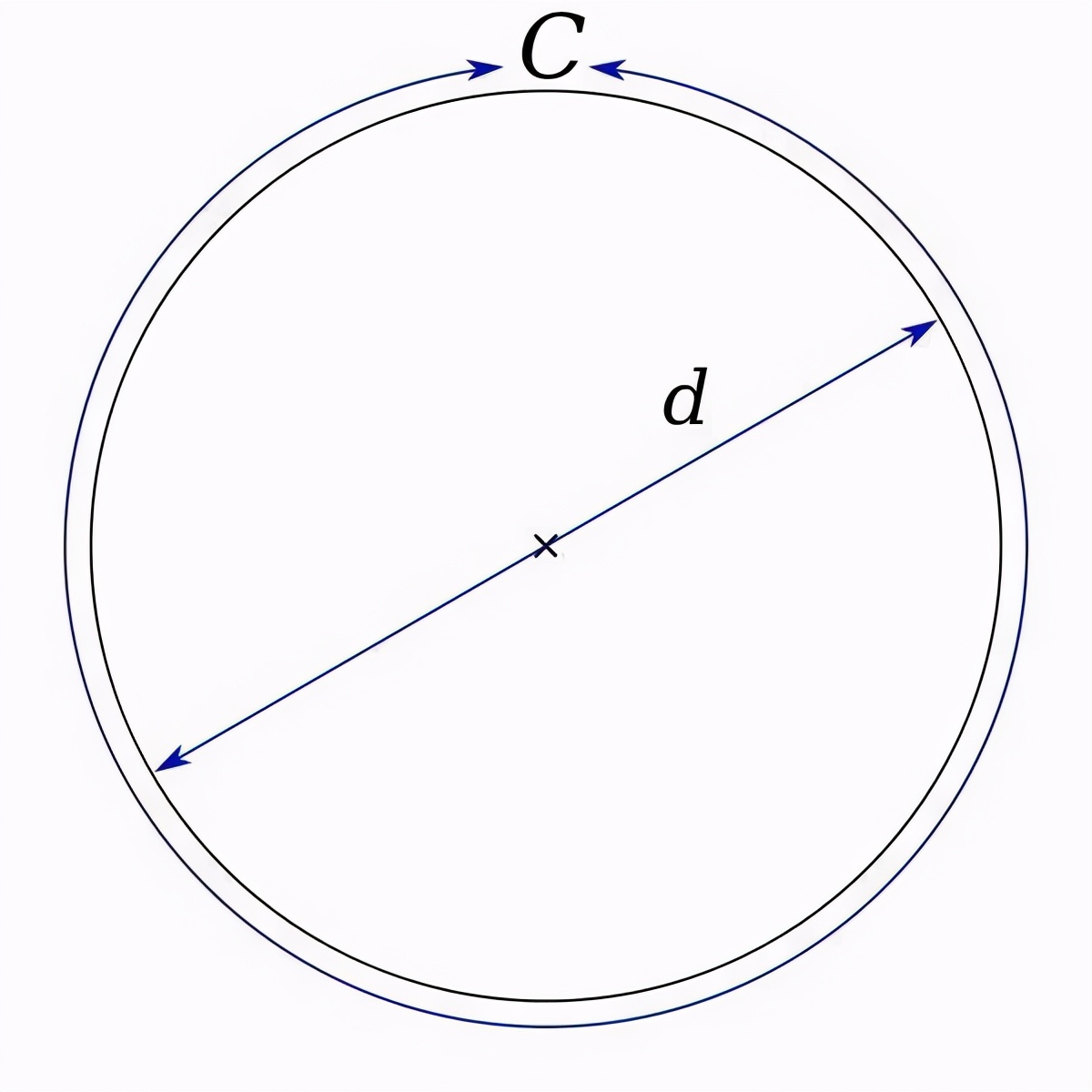
π，其實(shí)很簡(jiǎn)單，它就是圓周長(zhǎng)與直徑的比值。有一個(gè)非常簡(jiǎn)單的方法來(lái)理解圓周率派為什么是無(wú)理數(shù)，為什么永遠(yuǎn)算不出來(lái)。

這個(gè)方法是由圓的定義來(lái)決定的，你永遠(yuǎn)找不到也畫不出來(lái)一個(gè)真正的圓形。

比方說，如果圓的直徑是1，那么很容易計(jì)算出圓周長(zhǎng)就是π。這說明什么？說明了一個(gè)無(wú)限的概念，圓的周長(zhǎng)永遠(yuǎn)會(huì)無(wú)限地逼近一個(gè)值，但是永遠(yuǎn)到不了這個(gè)值，也就是說不存在真正意義上的圓。

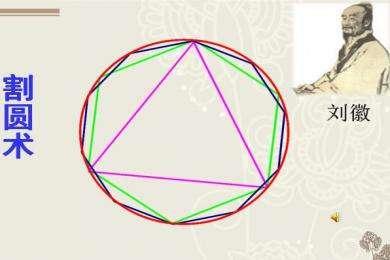
人類歷史上對(duì)于圓周率的計(jì)算一直沒有停止過，可以追溯到兩千多年前。古希臘數(shù)學(xué)家阿基米德能夠比較精確地計(jì)算出π在3.1408-3.1419之間，這已經(jīng)相當(dāng)精確了。我國(guó)古代數(shù)學(xué)家劉徽計(jì)算出來(lái)更精確的圓周率π，他利用的是割圓術(shù)，通俗地講，就是不斷地在圓內(nèi)部做內(nèi)接多邊形，讓多邊形周長(zhǎng)不斷逼近圓周長(zhǎng)，多邊形的邊數(shù)越多就越接近圓形。

劉輝用這種方法將圓周率π精確到了小數(shù)點(diǎn)后四位。

而著名數(shù)學(xué)家祖沖之繼承了劉徽的割圓法，更是將π精確到3.1415926到3.1415927之間，這個(gè)成就非常難得。

不過割圓術(shù)這種方法也有自己的缺陷，這種幾何方法有一定的缺陷，隨著多邊形邊數(shù)不斷變大，會(huì)變得越來(lái)越難以操作，因?yàn)槌叨葧?huì)越變?cè)叫?，精?xì)度要求越來(lái)越高。

而現(xiàn)代超級(jí)計(jì)算機(jī)的出現(xiàn)，讓人類計(jì)算圓周率π的位數(shù)有一個(gè)質(zhì)的突破，如今已經(jīng)計(jì)算到了31.4萬(wàn)億位。當(dāng)然計(jì)算機(jī)之所以算這么多位數(shù)，并不是驗(yàn)證π到底是不是無(wú)理數(shù)，更多的是驗(yàn)證計(jì)算機(jī)的性能。

π，是一個(gè)數(shù)學(xué)概念。不過對(duì)于熟悉物理的人來(lái)講，可能還有另外一個(gè)疑問。物理學(xué)上，確實(shí)存在最小的長(zhǎng)度單位，普朗克長(zhǎng)度。

雖然普朗克長(zhǎng)度很小，約等于1.616229×10^-35m，但再小也是一個(gè)數(shù)值。普朗克長(zhǎng)度的存在告訴我們，在現(xiàn)實(shí)中，事物并不是無(wú)限可分的，當(dāng)把一種事物分割到普朗克長(zhǎng)度，再分下去就沒有意義了。普朗克長(zhǎng)度有有意義的最小長(zhǎng)度單位。

普朗克長(zhǎng)度的存在是不是與無(wú)理數(shù)π相矛盾呢？

當(dāng)然不矛盾！

我們需要明白一點(diǎn)，數(shù)學(xué)和物理的區(qū)別，兩者并不是同一概念，并不能畫等號(hào)。說白了，數(shù)學(xué)只是人類認(rèn)知世界的一個(gè)工具罷了，是一個(gè)抽象概念。嚴(yán)格來(lái)講，數(shù)學(xué)并不屬于科學(xué)范疇。有些數(shù)學(xué)上的概念在物理和現(xiàn)實(shí)中并不成立。

我們都聽說過這種觀點(diǎn)：“一尺之棰，日取其半，萬(wàn)世不竭”。什么意思？將一根木棍無(wú)限分割下去，永遠(yuǎn)都分不完。

其實(shí)這種思想就是一種無(wú)限思想，我國(guó)古代對(duì)無(wú)限概念的理解和描述，在數(shù)學(xué)概念上確實(shí)是對(duì)的，但在現(xiàn)實(shí)和物理領(lǐng)域是不成立的。

那么如果圓周率被完全算出來(lái)會(huì)怎么樣？

簡(jiǎn)單講，我們?nèi)缃袼乃袛?shù)學(xué)體系都將崩塌。而很多物理學(xué)知識(shí)，都與圓周率π有非常緊密的聯(lián)系，這也意味著物理學(xué)大廈也將倒塌，人類幾千年來(lái)學(xué)些總結(jié)下來(lái)的知識(shí)幾乎全部需要修改。

說白了，我們需要從零甚至周圍的世界！

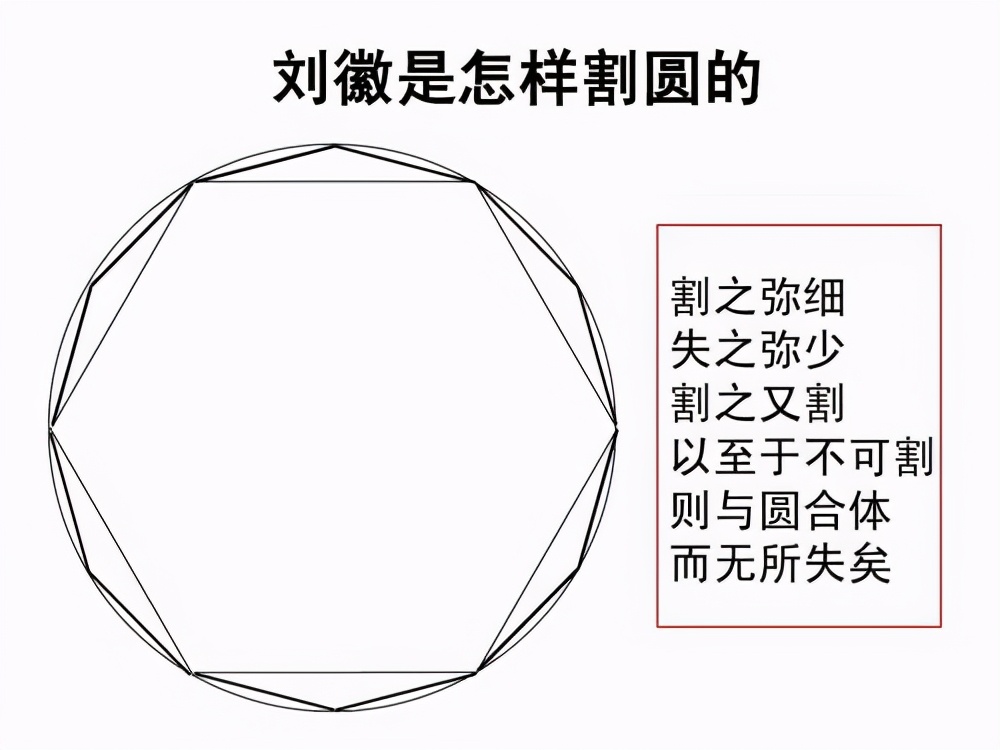
如果圓周率被完全計(jì)算出來(lái)，意味著圓其實(shí)就是一個(gè)“正多邊形”，意味著劉徽的割圓術(shù)在分割到一定程度將無(wú)法繼續(xù)分割。

同時(shí)，也意味著微積分概念是錯(cuò)誤的，那么現(xiàn)代人類利用微積分只是制造出來(lái)的集成電路也將不復(fù)存在，幾乎所有電子元件都將失效。

往大了說，組成物質(zhì)的分子原子的電子軌道可能變得不穩(wěn)定，物質(zhì)難以凝聚形成，整個(gè)宇宙都會(huì)被牽連，我們的宇宙將徹底崩塌！

這也太可怕了！

好在這種假設(shè)是沒有意義的，科學(xué)家早就證明了圓周率π的的確確是無(wú)理數(shù)，有多種方法可以證明，感興趣的朋友可以自行搜索下，并不難理解。