數(shù)字伴隨著人類社會(huì)的出現(xiàn)而出現(xiàn)，古時(shí)候人類為了便于記事，會(huì)在繩子上打個(gè)小結(jié)，又剛好人類有兩個(gè)手，每個(gè)手有五個(gè)手指。最初產(chǎn)生了1、2、3、4、5、6、7、8、9、10這樣的正整數(shù)。上古時(shí)期每個(gè)文明都發(fā)現(xiàn)了數(shù)字，只是阿拉伯?dāng)?shù)字最容易進(jìn)行計(jì)數(shù)，以至于現(xiàn)在國(guó)際通行阿拉伯?dāng)?shù)字，不過(guò)阿拉伯?dāng)?shù)字不是阿拉伯人發(fā)明的，而是有印度人發(fā)明阿拉伯人把它傳給了世界。

0的產(chǎn)生要到很久以后了，之前人們用空來(lái)表示0，但是很不方便，偶然的機(jī)會(huì)0這個(gè)數(shù)字產(chǎn)生了。這是數(shù)字由正整數(shù)擴(kuò)充到了0，0不是正整數(shù)它是最小的自然數(shù)。

隨著人類社會(huì)的發(fā)展，商業(yè)開(kāi)始出現(xiàn)，在使用數(shù)字時(shí)人們發(fā)現(xiàn)，當(dāng)用1頭豬換10只雞時(shí)，如果別人沒(méi)有10只只有8只，就記作欠兩只，欠兩只就是負(fù)整數(shù)。負(fù)數(shù)出現(xiàn)的更晚，直到和牛頓同時(shí)發(fā)現(xiàn)微積分的萊布尼茨還不認(rèn)可負(fù)數(shù)。負(fù)整數(shù)和自然數(shù)（0和正整數(shù)）共同構(gòu)成了整數(shù)。

數(shù)字的運(yùn)算隨著數(shù)字產(chǎn)生而產(chǎn)生，開(kāi)始只是加減運(yùn)算，對(duì)于較大重復(fù)累加的數(shù)字，加法顯得特別麻煩，乘除應(yīng)運(yùn)而生。分?jǐn)?shù)進(jìn)入歷史舞臺(tái)，整數(shù)和分子分母都是整數(shù)的分?jǐn)?shù)都有其具體形態(tài)，我們現(xiàn)在稱之為有理數(shù)。

無(wú)理數(shù)的誕生是數(shù)字發(fā)現(xiàn)史中最悲慘的，古時(shí)候有一個(gè)畢達(dá)哥拉斯學(xué)派，他們認(rèn)為萬(wàn)物皆數(shù)，畢達(dá)哥拉斯定理就是他發(fā)現(xiàn)的，就是我們學(xué)的勾股定理。他有一個(gè)學(xué)生希帕索斯在研究正方形的時(shí)候，如果邊長(zhǎng)是1，它的對(duì)角線的長(zhǎng)度應(yīng)該是√2，假設(shè)√2=a/b，則a、b同為整數(shù)且不可再約分，兩邊同時(shí)平方2=a^2/b^2，得出a^2=2*b^2，這時(shí)a^2一定是偶數(shù)a，也是偶數(shù)，且a^2能被4整除，兩邊同時(shí)約掉2，那么b^2是偶數(shù)，b也是偶數(shù)，至此a、b同時(shí)是偶數(shù)與假設(shè)不可約分相矛盾，進(jìn)而√2不是任何兩個(gè)整數(shù)的比。這與畢達(dá)哥拉斯的萬(wàn)物皆數(shù)相矛盾。無(wú)理數(shù)被發(fā)現(xiàn)，最后希帕索斯被無(wú)情的拋于大海中。

1844年著名數(shù)學(xué)家劉維爾寫出了下面這樣一個(gè)無(wú)限小數(shù)，a=0.110001000000000000000001000…（a=1/10^1!+1/10^2!+1/10^3!+…），并且證明a不可能滿足任何整系數(shù)代數(shù)方程，由此證明了它不是一個(gè)代數(shù)數(shù)。超越數(shù)被發(fā)現(xiàn)，超越數(shù)有無(wú)窮多個(gè)，但目前為止發(fā)現(xiàn)的超越數(shù)極其少，因?yàn)橐C明一個(gè)數(shù)是超越數(shù)是很難的。著名的π和e都是超越數(shù)。所有的超越數(shù)都是無(wú)理數(shù)，實(shí)代數(shù)數(shù)、實(shí)超越數(shù)共同組成了實(shí)數(shù)，當(dāng)然有理數(shù)和無(wú)理數(shù)也共同組成了實(shí)數(shù)。另外超越數(shù)的發(fā)現(xiàn)間接證明了尺規(guī)畫圓問(wèn)題。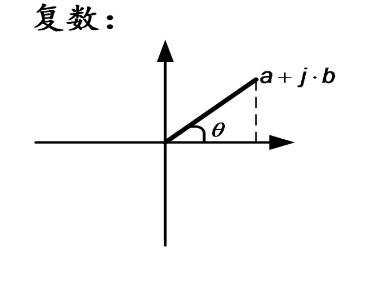

在解一元三次方程時(shí)，人們發(fā)現(xiàn)一元三次方程有三個(gè)解，大部分情況下會(huì)出現(xiàn)開(kāi)負(fù)數(shù)平方。17世紀(jì)著名數(shù)學(xué)家、哲學(xué)家笛卡爾首先引進(jìn)了虛數(shù)，后來(lái)人們用i來(lái)表示虛數(shù)單位。虛數(shù)i=√-1，完美解決了開(kāi)負(fù)數(shù)平方的問(wèn)題。實(shí)數(shù)和虛數(shù)共同組成了復(fù)數(shù)a+bi，當(dāng)b等于0時(shí)，a+bi是實(shí)數(shù)，其它情況都是虛數(shù)，其中當(dāng)a等于0時(shí)稱為純虛數(shù)。如果把復(fù)數(shù)放到坐標(biāo)系內(nèi)，我們會(huì)發(fā)現(xiàn)，實(shí)數(shù)只能有一條線a軸，純虛數(shù)有一條線bi軸，復(fù)數(shù)卻是整個(gè)平面。

數(shù)字的擴(kuò)充到復(fù)數(shù)就告別了一段落，目前為止人類發(fā)現(xiàn)的最高等級(jí)數(shù)就是復(fù)數(shù)。重溫一下數(shù)字發(fā)現(xiàn)的歷程，加法的需要發(fā)現(xiàn)了正整數(shù)，減法的需要發(fā)現(xiàn)了0和負(fù)整數(shù)，除法的需要發(fā)現(xiàn)了分?jǐn)?shù)，至此有理數(shù)全部到位。開(kāi)方計(jì)算發(fā)現(xiàn)了無(wú)理數(shù)，偶然機(jī)會(huì)發(fā)現(xiàn)了超越數(shù)，實(shí)數(shù)全部到位。因?yàn)槠渌?jì)算的需求發(fā)現(xiàn)了虛數(shù)，虛數(shù)和實(shí)數(shù)共同組成了復(fù)數(shù)，并建立了復(fù)平面坐標(biāo)系。

延伸講個(gè)小猜想，數(shù)字還會(huì)擴(kuò)充嗎？實(shí)數(shù)軸和每個(gè)實(shí)數(shù)都是一一對(duì)應(yīng)關(guān)系，并且任何兩個(gè)不相等的實(shí)數(shù)其中間必定有一個(gè)數(shù)。個(gè)人認(rèn)為這是一個(gè)悖論，假設(shè)實(shí)數(shù)a和b是兩個(gè)不同且緊緊相鄰的實(shí)數(shù)，則a和b中間只有一個(gè)數(shù)設(shè)為c，那么c這個(gè)數(shù)非常神奇，a和c、c和b一定是互不相等的數(shù)，但是它們中間不再有任何實(shí)數(shù)分布！所以0.9999……不等于1，哈哈哈！我不是民科，這個(gè)東西我還是不敢去推翻的。

前段時(shí)間看了一部科幻電影，說(shuō)的是超光速飛行是很簡(jiǎn)單的，導(dǎo)致很多宇宙文明都發(fā)現(xiàn)了，地球人卻錯(cuò)過(guò)了一次次的機(jī)會(huì)，但因禍得福，我們的科學(xué)技術(shù)均衡發(fā)展，其他宇宙文明卻被超光速飛行羈絆了其它科學(xué)技術(shù)。最終要來(lái)地球要飯吃。所以，我剛才的實(shí)數(shù)悖論會(huì)不會(huì)是被微積分給羈絆了思想？數(shù)字已經(jīng)由線發(fā)展到面，會(huì)不會(huì)發(fā)展到三維？歡迎點(diǎn)贊評(píng)論加關(guān)注。