向量在高中數(shù)學(xué)中最重要的是作為工具的作用。高考中，向量難度一般不大，應(yīng)用廣泛，既可以考純向量，在高考中常考一個(gè)5分的小題；向量也可以與三角、解三角形、平面幾何、立體幾何、圓錐曲線等知識(shí)結(jié)合出題。既可以考小題，也可以考大題。

向量?jī)?nèi)容簡(jiǎn)而言之為：三三四五，既三種運(yùn)算形式；三個(gè)標(biāo)志性成果；四個(gè)運(yùn)算；五種應(yīng)用。

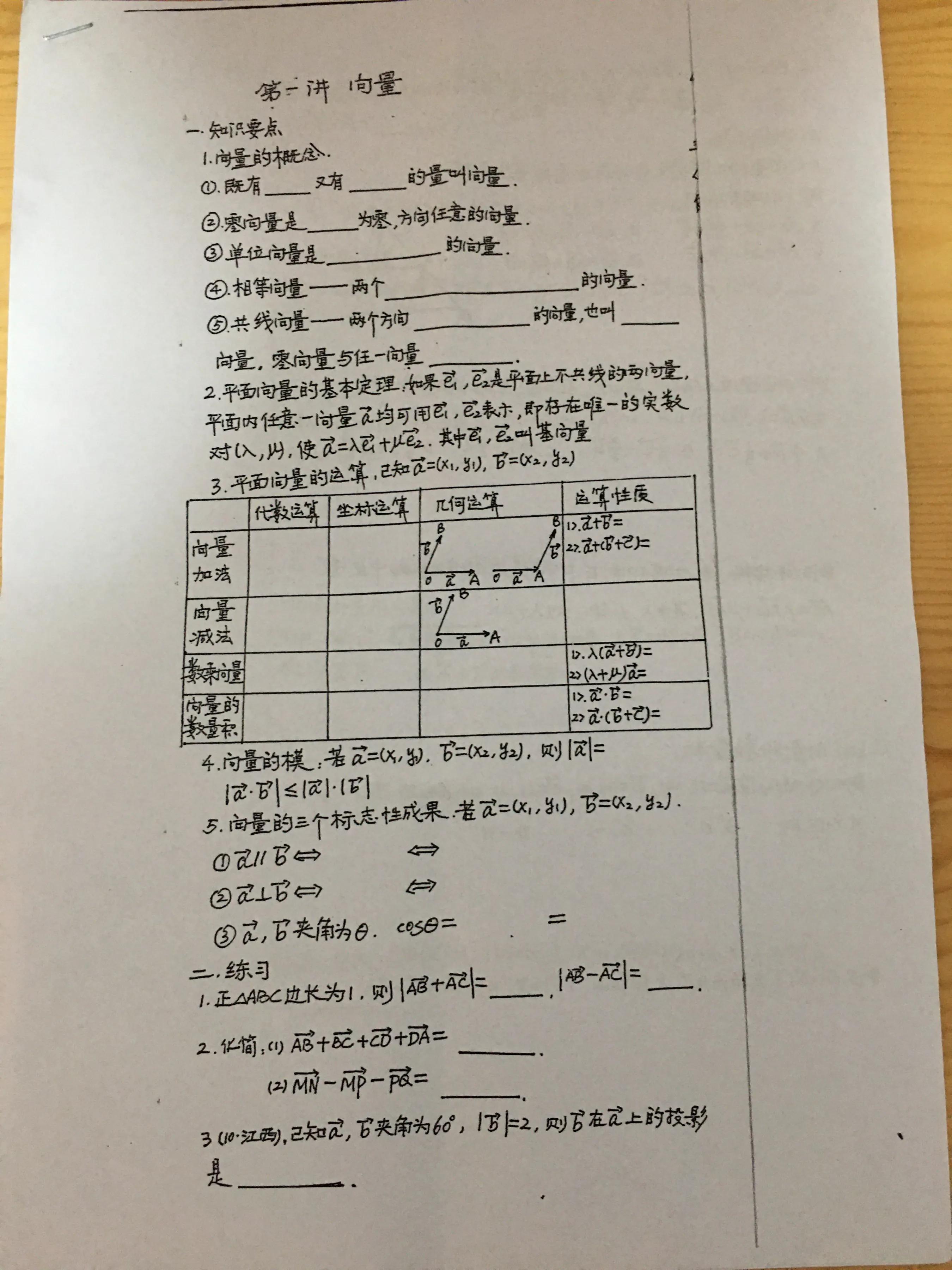
（一）三種運(yùn)算形式

向量的運(yùn)算有三種：幾何運(yùn)算，代數(shù)運(yùn)算和坐標(biāo)運(yùn)算。

最簡(jiǎn)單的是坐標(biāo)運(yùn)算；第一個(gè)難點(diǎn)是：幾何運(yùn)算，尤其是平面向量的基本定理，主要是利用向量加法和減法及數(shù)乘向量的幾何意義，將平面上任一向量用一組基底向量表示；第二個(gè)難點(diǎn)是幾何運(yùn)算和代數(shù)運(yùn)算的綜合運(yùn)用。

（二）向量的三個(gè)標(biāo)志性成果

向量的三個(gè)標(biāo)志性成果為：平行，垂直和夾角。

向量平行的充要條件是坐標(biāo)成比例。

向量垂直的充要條件是數(shù)量積等于零，既橫坐標(biāo)之積與縱坐標(biāo)之積的和為零。

兩向量的夾角的余弦等于兩向量的數(shù)量積與兩向量的模的積的比。

以上三種運(yùn)算是高考中純向量題中多次考試的內(nèi)容。

（三）向量的四種運(yùn)算

四種運(yùn)算：向量的加法、向量的減法、數(shù)乘向量和向量的數(shù)量積。前三種運(yùn)算結(jié)果仍為向量，向量的數(shù)量積為實(shí)數(shù)。

向量的加法、減法和數(shù)乘向量的坐標(biāo)運(yùn)算就是坐標(biāo)相加、減和數(shù)乘；向量的數(shù)量積的代數(shù)運(yùn)算是兩向量的模與其夾角的余弦之積，坐標(biāo)運(yùn)算是兩向量的橫坐標(biāo)之積與縱坐標(biāo)之積的和。

向量的數(shù)量積的代數(shù)運(yùn)算應(yīng)用較多，常見(jiàn)題型有求向量多項(xiàng)式的乘積及有關(guān)求模的問(wèn)題。此類題在高考中反復(fù)考查。務(wù)必熟練掌握。

（四）向量的五種應(yīng)用

應(yīng)用一：向量與三角

見(jiàn)例14，例15，用數(shù)量積的定義，占一分，最終變成三角函數(shù)的問(wèn)題。

應(yīng)用二：向量與解三角形

三角形中出現(xiàn)向量運(yùn)算或表述。

應(yīng)用三：向量與平面幾何

可用向量證明平面幾何中的平行和垂直問(wèn)題，也可求夾角，見(jiàn)資料上的例13。

應(yīng)用四：向量與立體幾何

主要出現(xiàn)在立體幾何大題的第二問(wèn)。求三種空間角。詳情見(jiàn)3月15日本人的微搜索。

應(yīng)用五：向量與圓錐曲線

還是將向量作工具穿插在圓錐曲線的大題或者小題中。

春季開(kāi)學(xué)，高一一開(kāi)始就學(xué)向量，本內(nèi)容可供高中各年級(jí)的同學(xué)參考復(fù)習(xí)。