周蒙問了我兩道題

前言:本文作者是龍盤湖國際學(xué)校許莎老師�����,曾經(jīng)的一位學(xué)生,現(xiàn)就讀重點高中�����,跑回來問了許老師兩道高中數(shù)學(xué)題���,以這兩道題的解讀為例,展現(xiàn)研題的部分過程,原文如下:
周蒙現(xiàn)在在夷陵�����,以前我在六班替老王上過一節(jié)課���,他們就認識了我��,然后今年過年來問了我兩道題�����。
1.棱長為4的正方體有蓋容器內(nèi)放入兩個體積相同的金屬小球(蓋子能夠閉合)��,則小球半徑的最大值為( )
A. 4-2√2 B.2√6-2√3 C.1 D.3-√3
關(guān)于這個題�,我的第一反應(yīng)是����,他不會畫圖,所以不會計算����。尤其是球不會畫,球在立體圖形中不好畫��。然后我自己想了一下,我的疑惑是����,這兩個球的球心連線會不會在正方體的體對角線上呢��?其實我自己也不太好想象這個圖的平面圖像是什么樣。于是我找了兩個健身球和一個盒子擺了一下��。

我發(fā)現(xiàn)當(dāng)盒子為長方體的時候球心連線肯定不在體對角線上��。那么當(dāng)盒子為正方體時���,球心連線會不會在體對角線上呢����?
網(wǎng)友的答案是這樣的��,當(dāng)然沒有畫圖,因為不好畫�����。只是用文字進行了敘述��。
提問:正方體內(nèi)有兩個球相外切且又分別與正方體內(nèi)切���,為什么兩球的球心在體對角線上
寫出詳細的證明過程來�。
回答:兩球與正方體內(nèi)切說明兩球的圓心分別到切面的距離相等(為圓的半徑)正方體體對角線上的點到最近的三個面的距離相等(當(dāng)點是體心時,到六個面距離都相等)所以兩個球的球心在體對角線上�����。
根據(jù)網(wǎng)友的回答���,我畫出了這樣的圖來進行證明。
過P點作面A’B’C’D’的垂線P’G��,作面AA’B’B的垂線PE���,作面BB’C’C的垂線PF
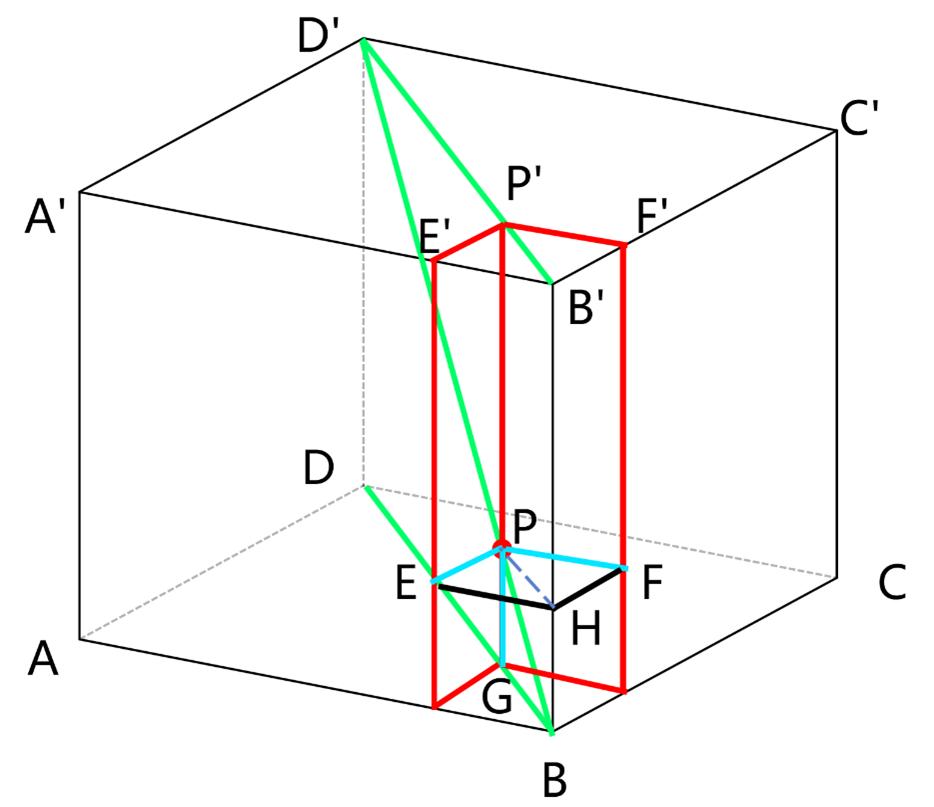
∵P在BD’上
∴P’在D’B’上
∵D’B’為∠A’B’C’的角平分線
∴P’E=P’F’
∴PE=PF
∵PG∥DD’
∴PG:DD&39;=BG:BD
∵BD=√2DD&39;
∴BG=√2PG=PH=√2PF
∴PG=PF
∴PG=PF=PE
∴點P為球心
∴與正方體三個面內(nèi)切的球心都在體對角線上
于是這個題就很好畫出正方體對角面上的平面圖,從而開始計算����。
在畫圖的過程中�����,我第一次犯了一個錯誤��。
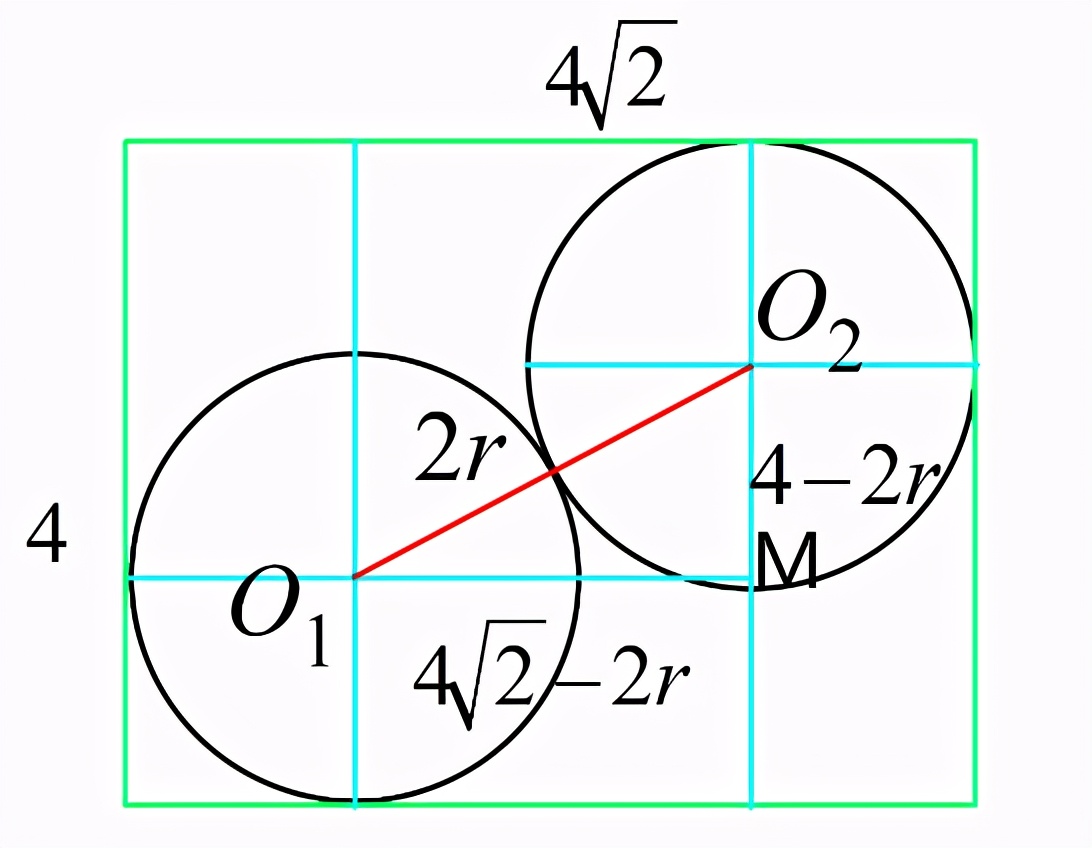
我把圖畫成了這樣�,根據(jù)勾股定理,列出方程為:
r2-(4√2+4)r+12=0
這個方程解出來沒有選項的結(jié)果����。但是看這個圖好像沒有
表達上的錯誤。于是我覺得肯定是我的圖畫錯了。
錯誤在哪呢���?這個圖看上去也挺科學(xué)的啊���。

于是我又仔細看了一下第一個實物圖。
發(fā)現(xiàn)了問題的所在���,原來我這個平面圖畫的是實物圖
的俯視圖����,而從對角面看過去����,圓的左右與側(cè)棱是沒有
相切的��。這也是同學(xué)們?nèi)菀追傅腻e誤,直觀圖變平面圖
很容易被我們所看見的迷惑����。
經(jīng)過修改����,我畫出了正確的平面圖像����。
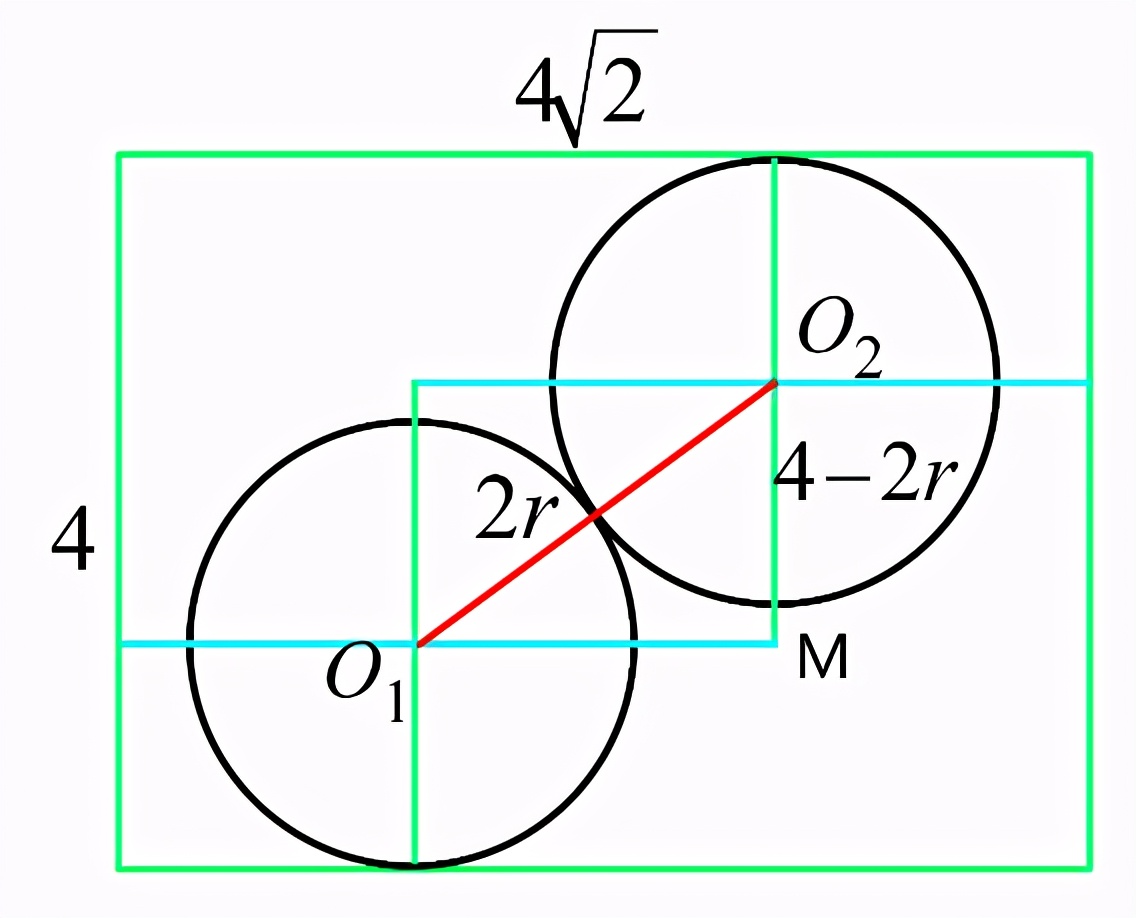
∵△O1O2M∽△BD’D
∴
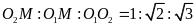
∴
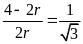
∴
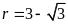
在我的不懈努力下終于把對角面圖畫出來了~
學(xué)生肯定無法在紙上畫出立體圖形,那么我們
就必須讓學(xué)生先從實物觀察入手��,然后通過抽象思維
建立模型,把立體圖形轉(zhuǎn)化為平面圖形�����。
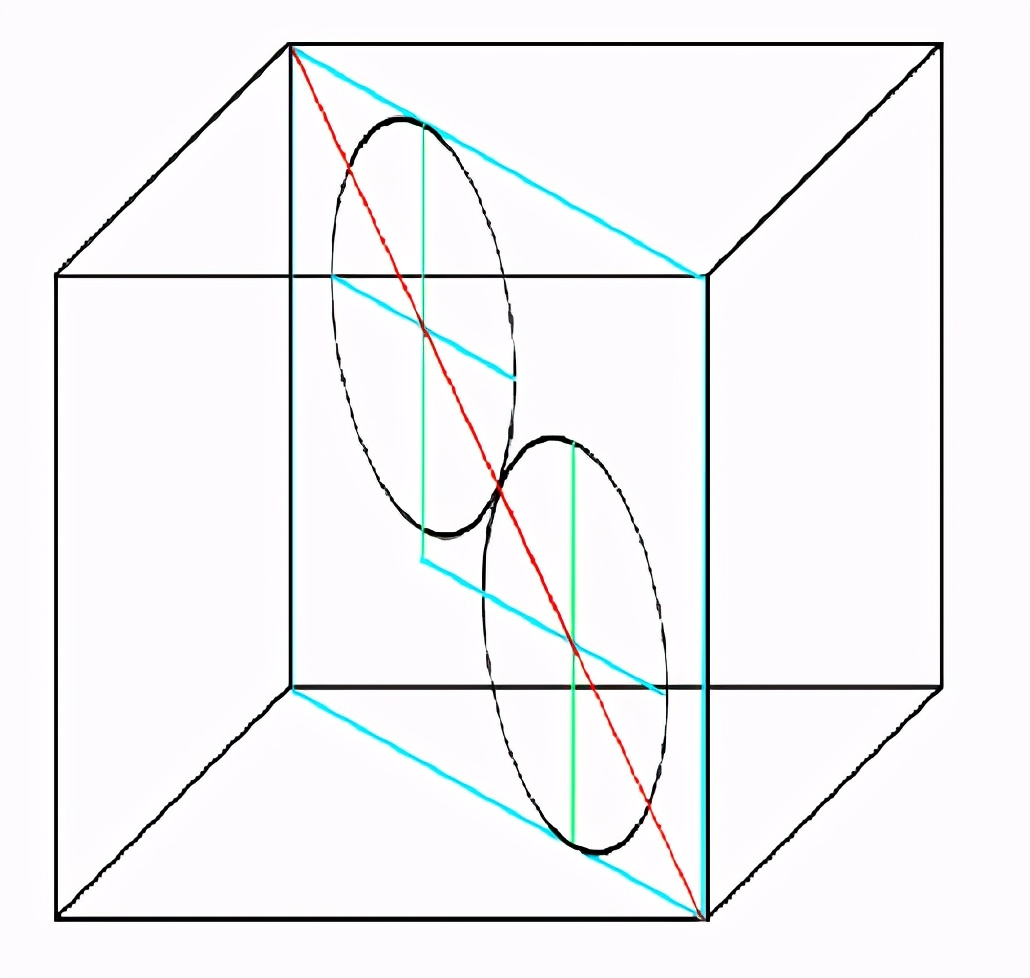
因此我認為,幾何學(xué)習(xí)��,尤其是立體幾何的學(xué)習(xí)����,
動手操作和實際觀察是非常重要的。
數(shù)學(xué)建模應(yīng)該是:實際→數(shù)學(xué)模型→實際
而不是沒有任何感知就讓學(xué)生把圖畫出來進行計算���。
后面兩幅圖是我使出了洪荒之力才畫出來的~
太棒了~
希望所有的同學(xué)們能夠有認知能力和畫圖能力,
PS:用斜二側(cè)畫法才是最好看的����!
所以在七年級學(xué)習(xí)立體圖形的時候就要貫徹斜二側(cè)畫法
只有斜二側(cè)畫法才能最有立體感且不會讓有的線被擋住�����。
2.已知函數(shù)
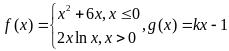
,若

與
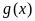
的圖像有4個不同的交點���,則實數(shù)k的取值范圍是 。
這個題目典型的數(shù)形結(jié)合思想��,要畫函數(shù)圖像���,他說他不會畫第二個函數(shù)的圖像����,這個是典型的冪函數(shù)和對數(shù)函數(shù)乘積的形式的圖像�。在沒有學(xué)導(dǎo)數(shù)之前�,沒有辦法通過導(dǎo)函數(shù)的正負來確定原函數(shù)的增減性����。那么我們可以通過一些直觀的判斷來大致確定函數(shù)圖像�����。
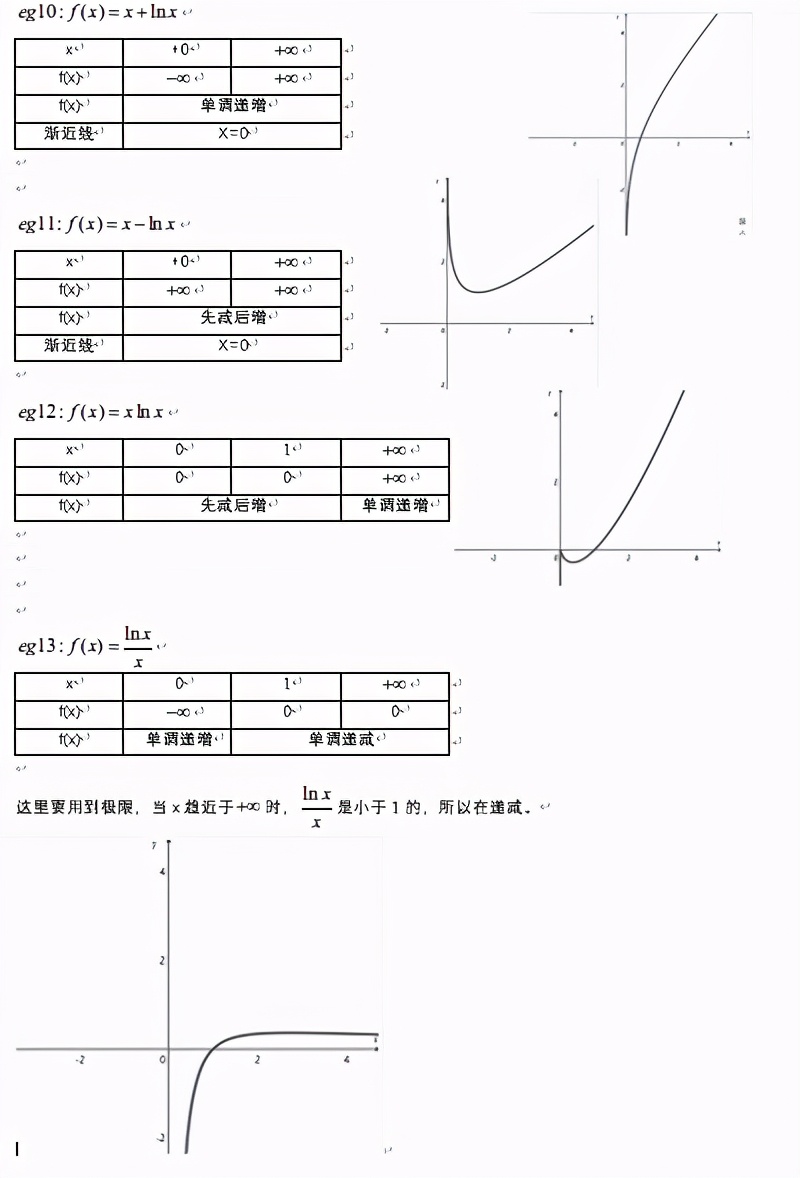
由觀察得當(dāng)x=0的時候����,帶入第1式得f(x)=0,那么當(dāng)x=0時���,帶入第2式,也是可以得到f(x)=0的��。有的同學(xué)就會說��,第2個式子取不到0啊�,事實上��,這只是為了定義域表示的不重復(fù),我們知道lnx的x為0的時候���,函數(shù)值是趨近于負無窮大的�����,那么2xlnx在x=0的時候,它的值也是為0的�����。所以說f(x)也是一個在全體實數(shù)上連續(xù)的函數(shù)����。因此我們能很快的知道當(dāng)x>0時在x=1的時候f(1)=0��。所以說函數(shù)的兩個零點之間一定是先遞減再遞增,因為當(dāng)x在(0,1)之間時f(x)<0���。這樣我們就可以大致畫出函數(shù)圖像了�。
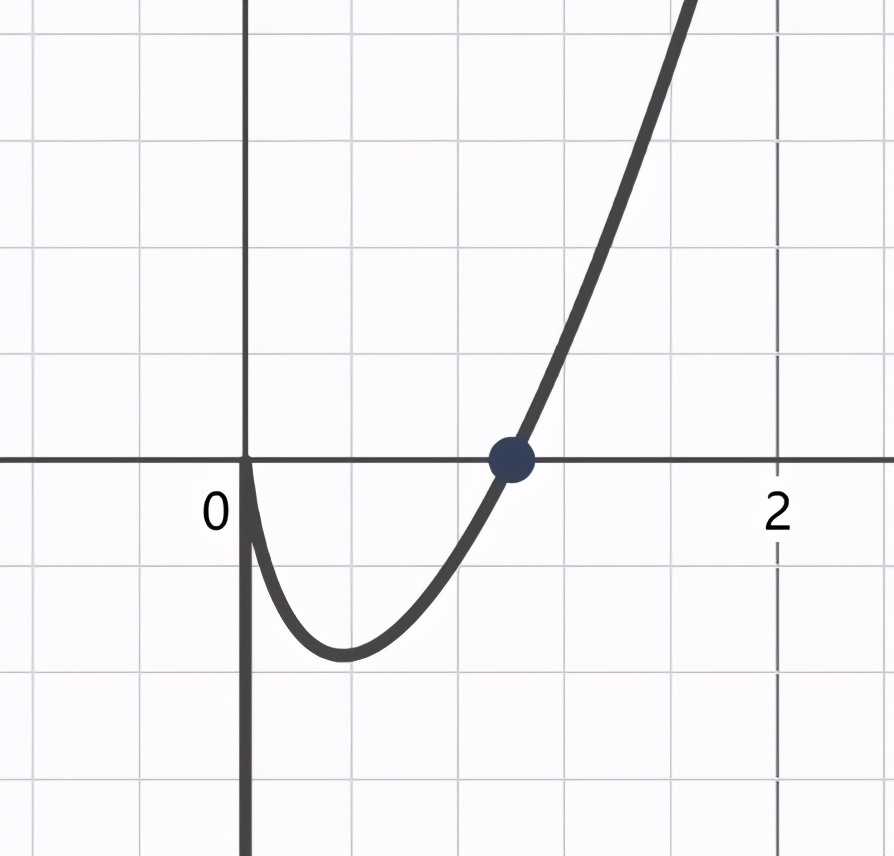
對于一般函數(shù)函數(shù)的圖像的畫法����,除了求導(dǎo),因為求導(dǎo)比較耗時�,有時候有的求導(dǎo)了之后也無法計算���,所以我們需要有能夠?qū)竞瘮?shù)的圖像有大致推斷的能力�����。這在必修1學(xué)習(xí)完第2章就應(yīng)該具備這樣的能力。然而大多數(shù)同學(xué)把基本初等函數(shù)的圖像當(dāng)做一個一個孤立的內(nèi)容去學(xué)習(xí)�����,沒有找到他們之間的聯(lián)系�。所以感覺做函數(shù)的題目舉步維艱����,無法判斷單調(diào)性�����。所以就會有畏難情緒����。大多數(shù)時候���,我們的恐懼是來自于那些對未知事物的不確定性。對于函數(shù)圖像的不確定性就是學(xué)習(xí)函數(shù)的最大障礙�����。
下面我們來一起總結(jié)一下如何推斷一些常見的函數(shù)的圖像情況��。
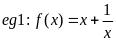
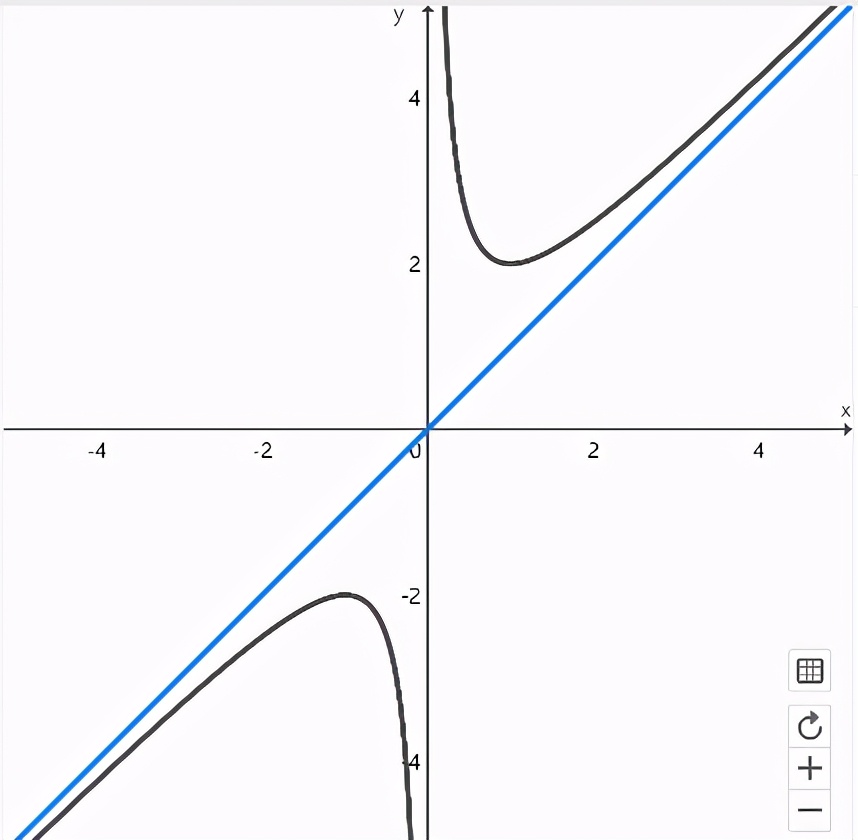
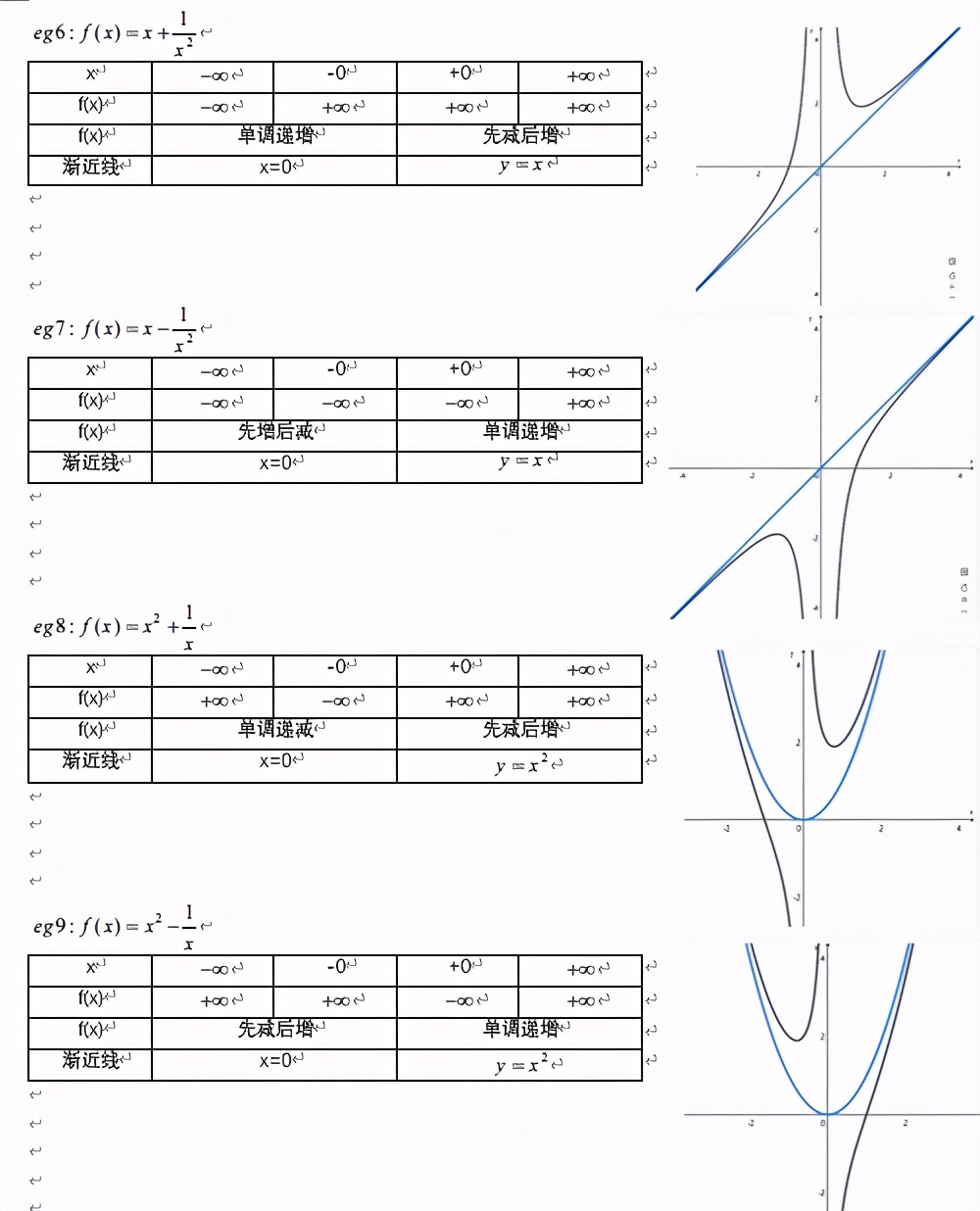
這個函數(shù)是我們學(xué)過的對勾函數(shù)��,是一個雙曲線,也叫“耐克函數(shù)”�。

這是以x=0和y=x為漸近線的一組雙曲線���,有最值���,無零點。
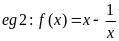
,如果把對勾函數(shù)的中間改成-號��,圖像會變成什么樣呢���,很顯然�,這個函數(shù)就會有兩個零點。分別為1或-1�����。當(dāng)x>0時���,x當(dāng)然是趨近于+∞,1/x是趨近于+0,因此����,x-1/x是趨近于+∞。當(dāng)x趨近于+0的時候��,1/x趨近于+∞�����,那么就說明x-1/x=0-(+∞)�,因此����,x-1/x趨近于-∞���。那么我們就可以判斷出,當(dāng)x>0時�,函數(shù)是由-∞遞增到+∞�,當(dāng)x=1時有一個零點���。而f(x)為奇函數(shù),因此當(dāng)x<0時����,函數(shù)單調(diào)遞減,當(dāng)x=-1時有一個零點�。這樣我們就畫出了f(x)的圖像���。
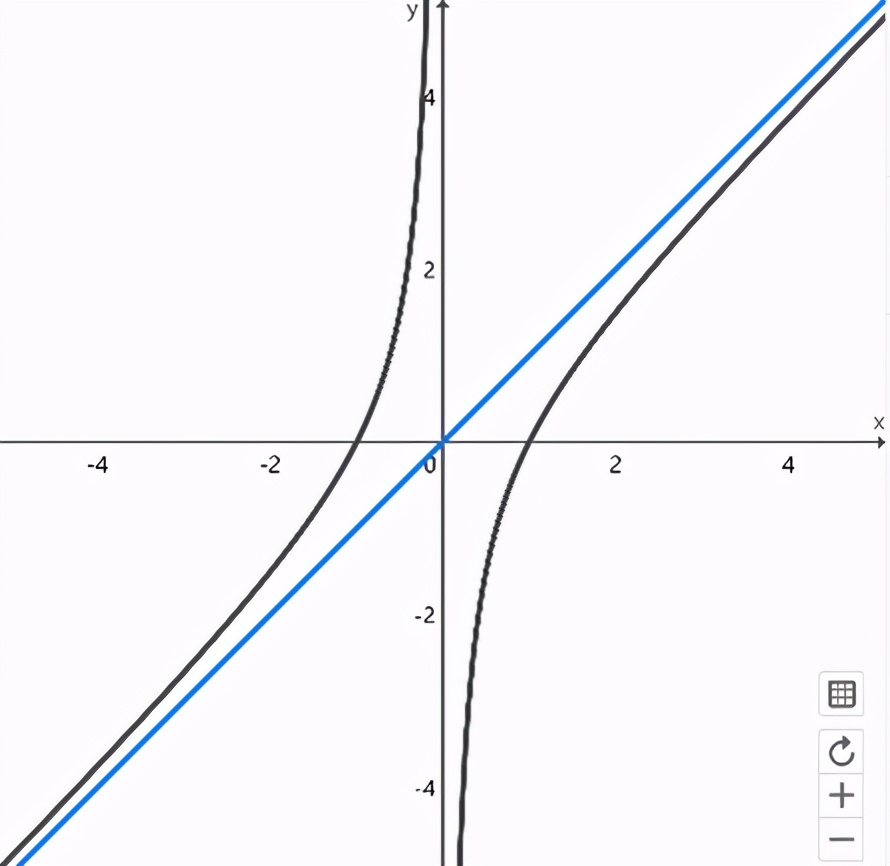
所以我們總結(jié)一下推斷函數(shù)圖像的方法:
微信公眾號:愛數(shù)學(xué)做數(shù)學(xué)

